My Idiot Brain Ruined My School’s NAPLAN average, But Bootstrapping Could Have Saved it

Creative writing has never been my forte, however, no attempt was worse than my 5th Grade NAPLAN test. My score was so poor I suspect the examiners were concerned I would never turn out to be a functional adult capable of basic literacy. Unfortunately for my school, typical sample metrics like averages and standard deviation can be heavily skewed by a single student who thinks spelling is a waste of time, and writing out the plot of last nights fever dream makes for good literature. This issue for my school could have been fixed if, rather than using typical sample statistics, the NAPLAN examiners employed bootstrapping.

What is Bootstrapping?

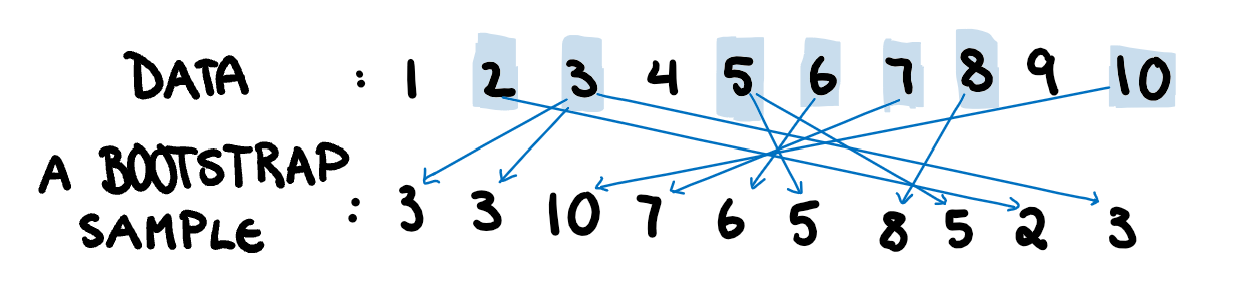
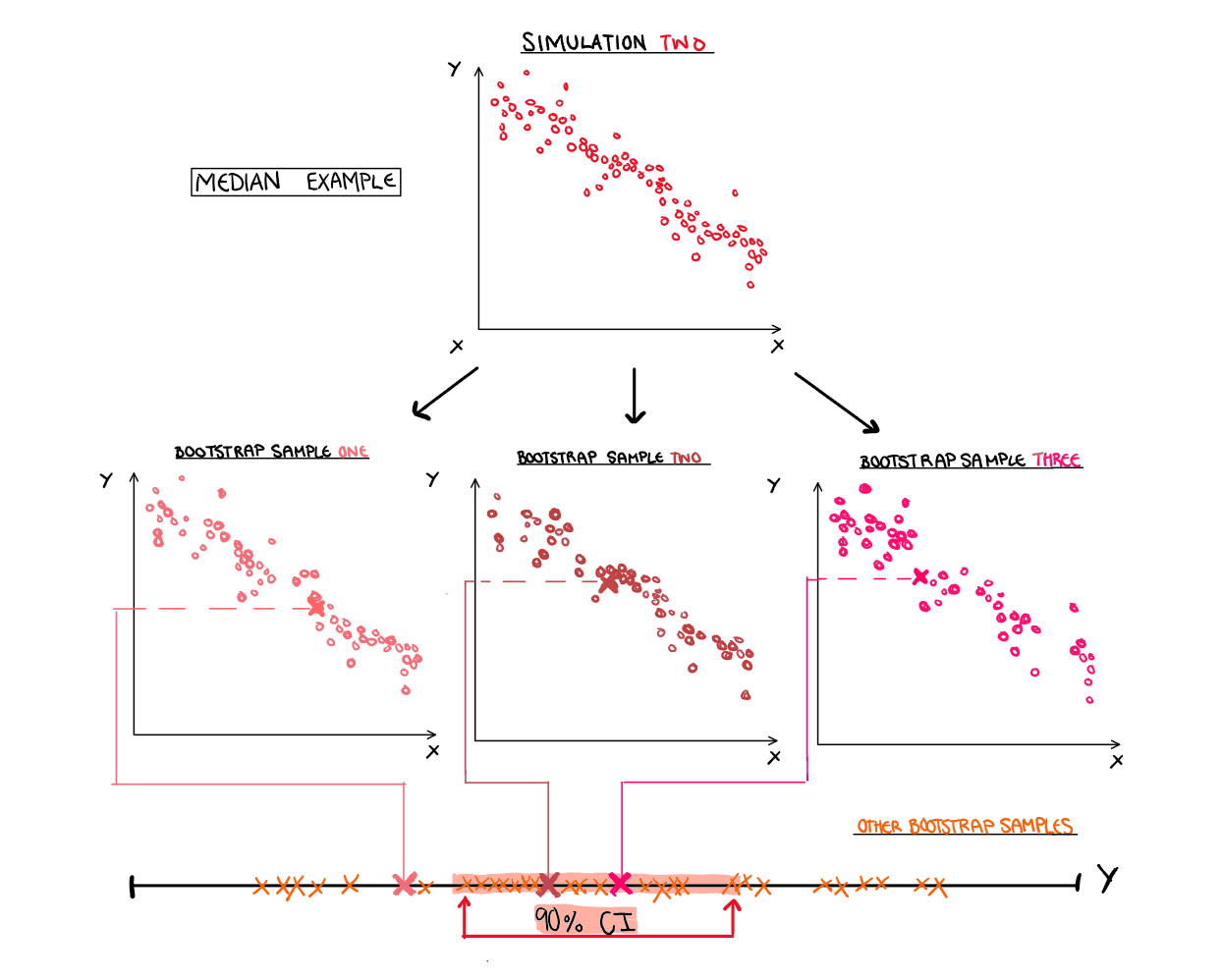
Bootstrapping is a versatile tool that can be used to find estimates of variance when they aren’t easily found analytically. This could be due to it being an uncommon statistic, or due to sampling from a strange distribution. Essentially, we sample from our dataset, with replacement, to make a new dataset that is the same size, as illustrated below. It works similarly to simulation, and understanding where simulation and bootstrapping diverge make the limitations and applications easier to understand.

Simulation and Bootstrapping

For those of us in statistics, simulations are a useful tool and not just something your pseudo-intellectual friend brings up after watching a Neil deGrasse Tyson documentary. When an analytical solution is unavailable to us (or if the math isn’t worth it) a simple estimate with a simulation can go a long way. Bootstrapping is closely related to simulation and outlining their similarities and differences makes it easier to understand the main ideas of bootstrapping.

If our data creation process was forced into the context of a family tree, simulated data would be the parent of the bootstrap sample. A simulation of a simulation if you will. If we illustrate this, we need to start with our random process, the true data generating process that we assumes exists but can never truly know. This process creates our data (or simulation if we are working artificially) which turn creates our bootstrapped samples.

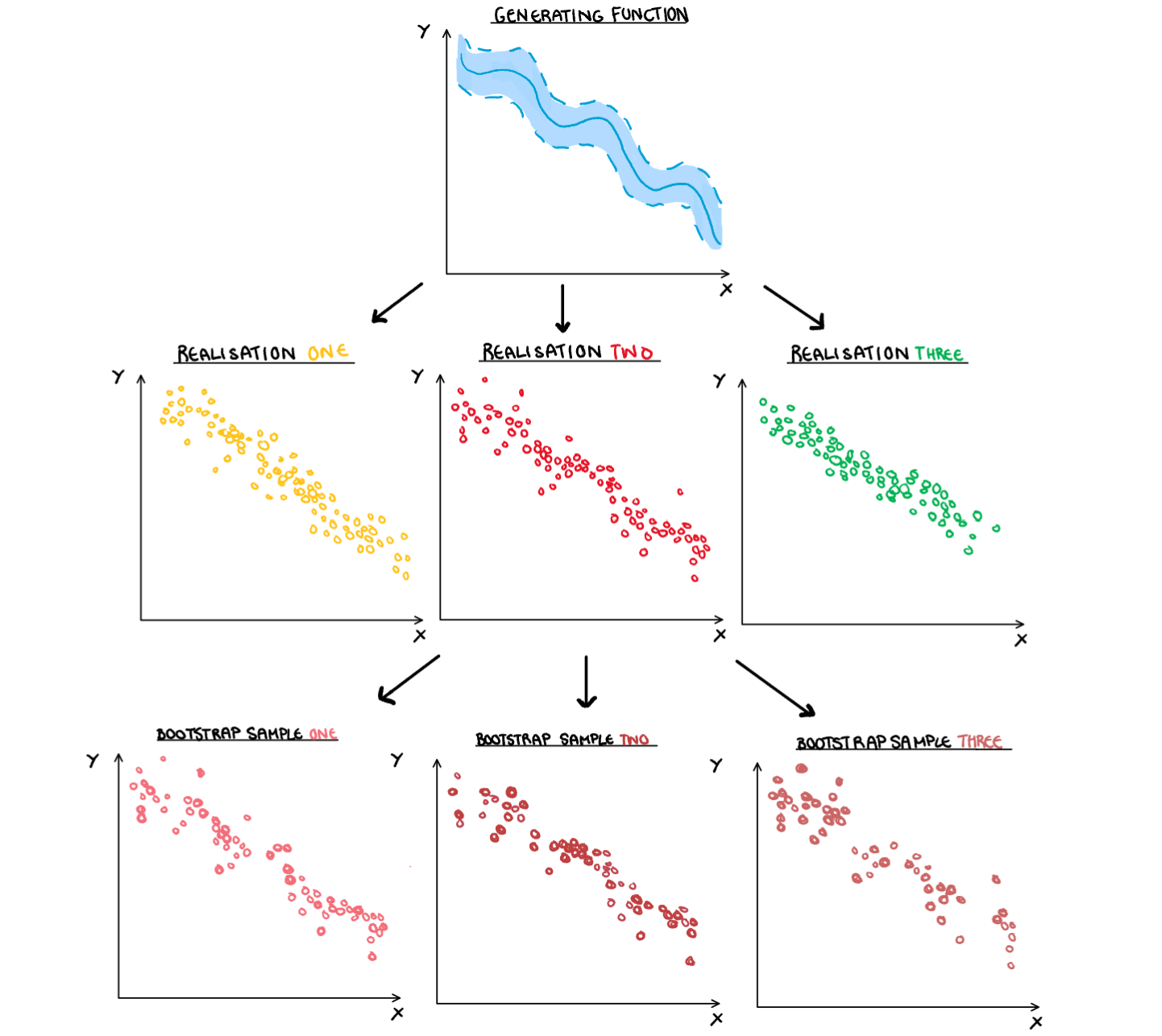
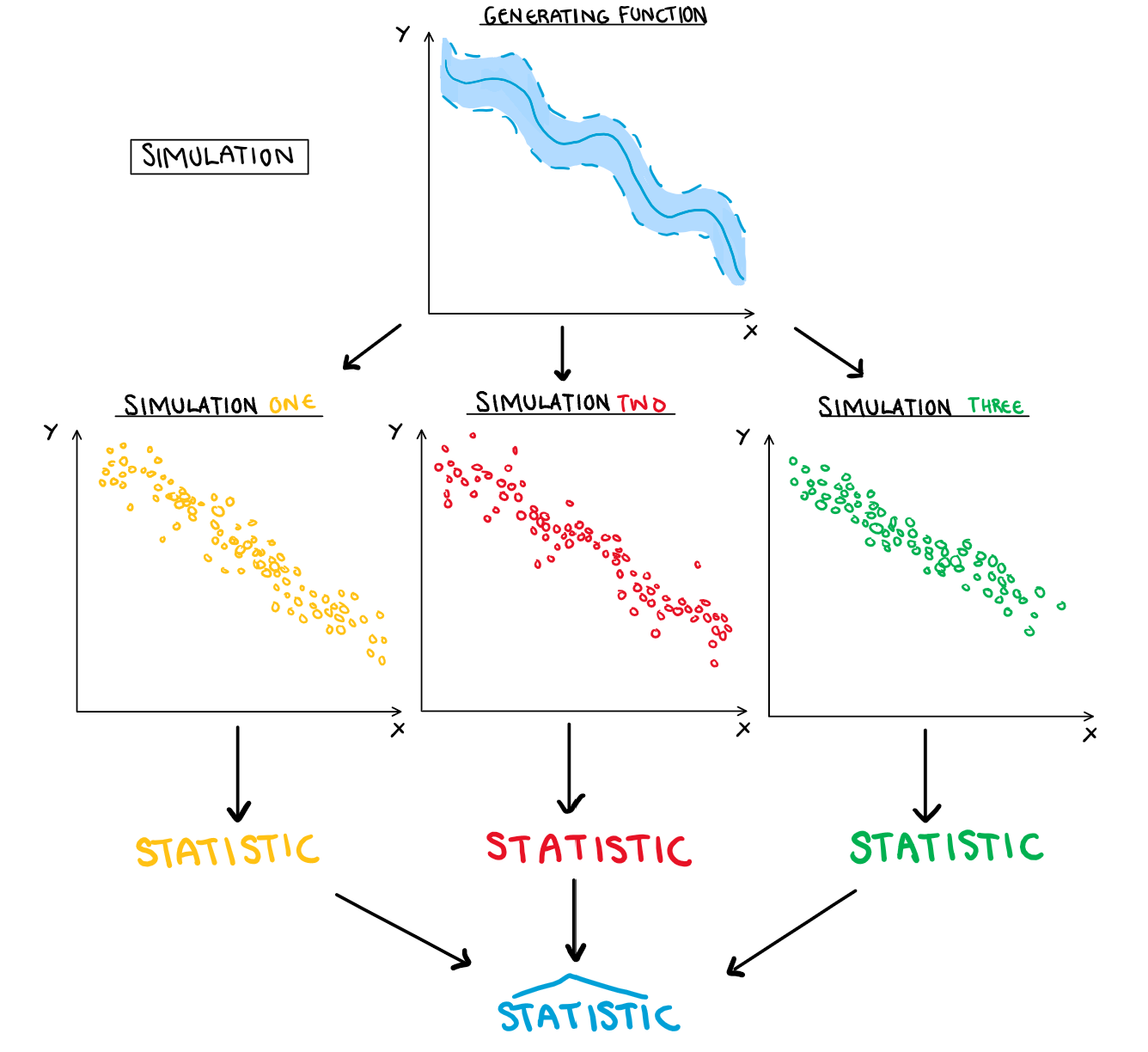
For a simulation, each observation is an independent trial generated from the true data generating process. As we generate more and more of these simulations, their behaviour (and thus statistics) will on average approach the true distribution. So we can average them to make estimates for the underlying process.

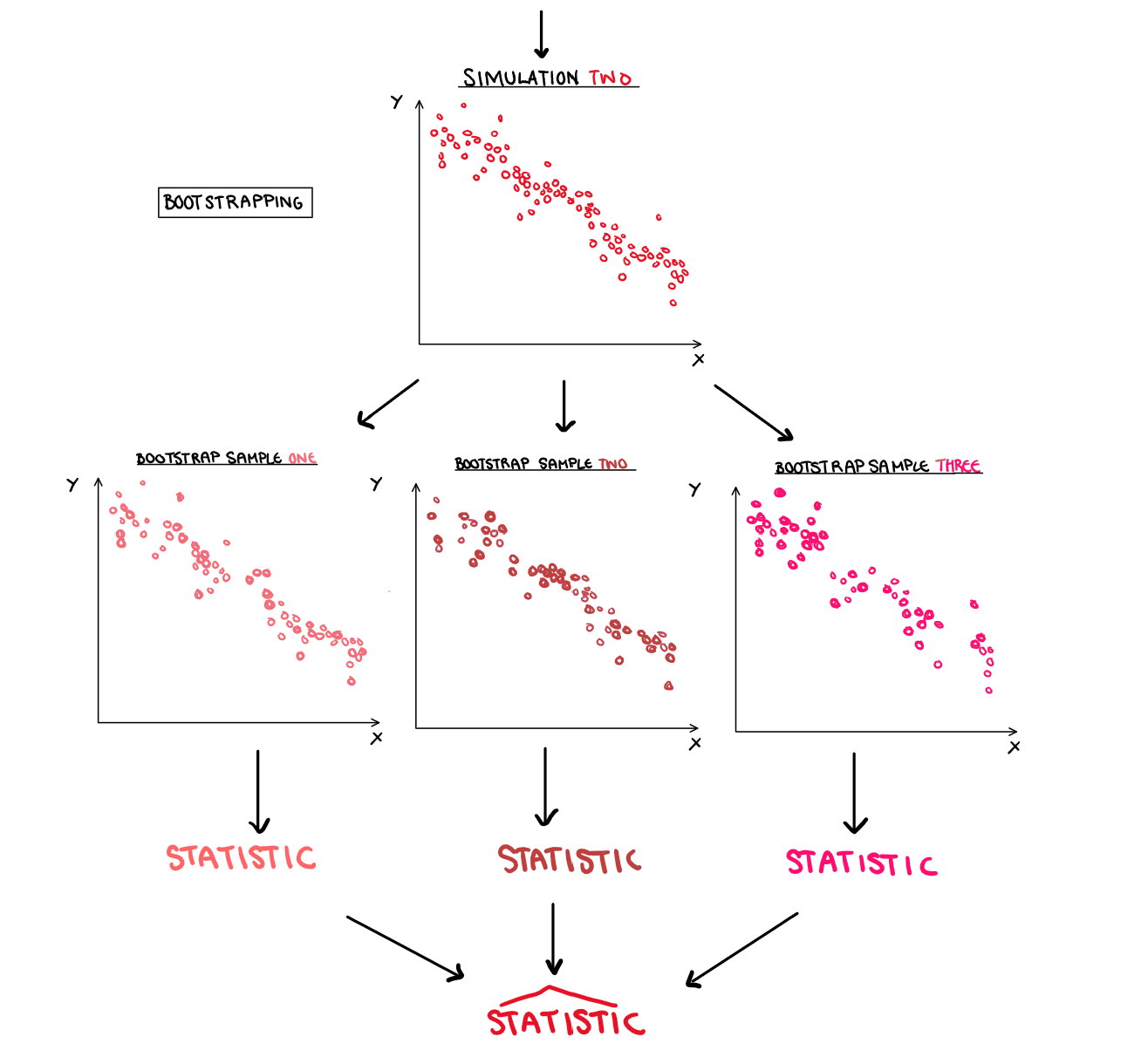
Bootstrapping is a little different but follows a similar idea. Instead of the source being a generating function, it is one of the simulations. To replicate the effect of independent trials, we sample with replacement from the data and generate a new dataset. This new dataset is essentially a simulation of that original simulation. Much in the way that simulation takes one step back and looks at the true relationship, bootstrapping takes one step back and can be used to estimate statistics in the data.

The Limitations of Bootstrapping

Bootstrapping is a simple trick that allows us to fabricate new samples from our data to understand the variance of our statistic. This process, however, only allows us to take one step back in the chain of simulation. Bootstrapping from a dataset only estimates the statistics from that dataset, going further and making estimates for the true underlying process would require additional natural data. More data through bootstrapping won’t cut it.

Here you may throw up your hands at the futility of trying to estimate anything as you stare in the mirror and ask your refection why you chose statistics instead of following your childhood dream of running an ice cream shop. Lucky for us, data analysis evolved from mathematics with the key goal to estimate the impossible, using an age old technique called lowering our standards.

Really the underlying data generating process is more of an idea than something you can touch. So the limitation isn’t that limiting. If you just change your goal to understanding the dataset, an endeavour that is more practical really, bootstrapping works just fine.

Estimating Confidence Intervals

How can we use bootstrapping for something helpful, like estimating a confidence interval? Well, the process is surprisingly simple, and we have already done most of the work. After you have taken your bootstrapped samples and estimated your statistic of interest for each, you simply order them and take the values that lie on the percentile boundary. That’s it. You want a 90% confidence interval with 100 bootstrap samples? Well take the 100 bootstrapped sample statistics, order them, and the value range between the 5th and 95th observations is your 90% confidence interval. It’s that simple.

Using my Poor English Grades For an Example

When I was a child, I did so badly in the year 5 NAPLAN writing that the school insisted on moving me from advanced, to remedial English. My paper, as my teacher explained to my mother, seemed to be a summarised plot of the anime “Full Metal Alchemist”, written in one sentence that spanned several pages, with no punctuation, and mostly incorrectly spelled words. This was coming in hot after my older brother, three years my senior, had also failed a large portion of his NAPLAN tests because he was “too busy thinking about his imaginary Pokémon” to answer the questions, and randomly filled in bubbles in the last 5 minutes. We are going to use my attack on the advanced class average as an example in bootstrapping.

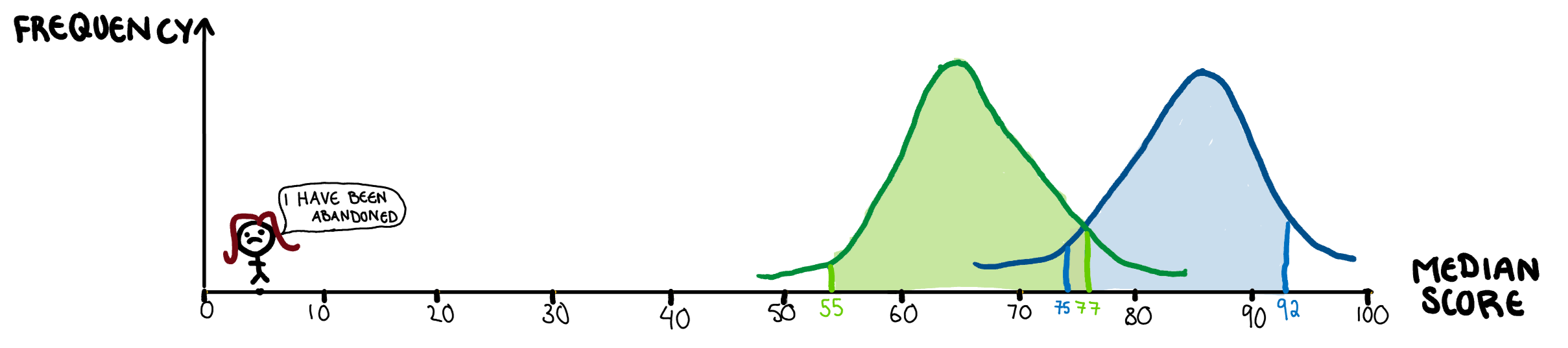
Lets say the advanced class and the regular class both have 5 students each (they didn’t but drawing those stick people gets tiring). All these students have an associated test score, and the staff want to compare the two classes. Simply using the mean of the two classes will cause issues, since the mean is susceptible to be skewed by outliers, and my idiot paper is a big outlier.

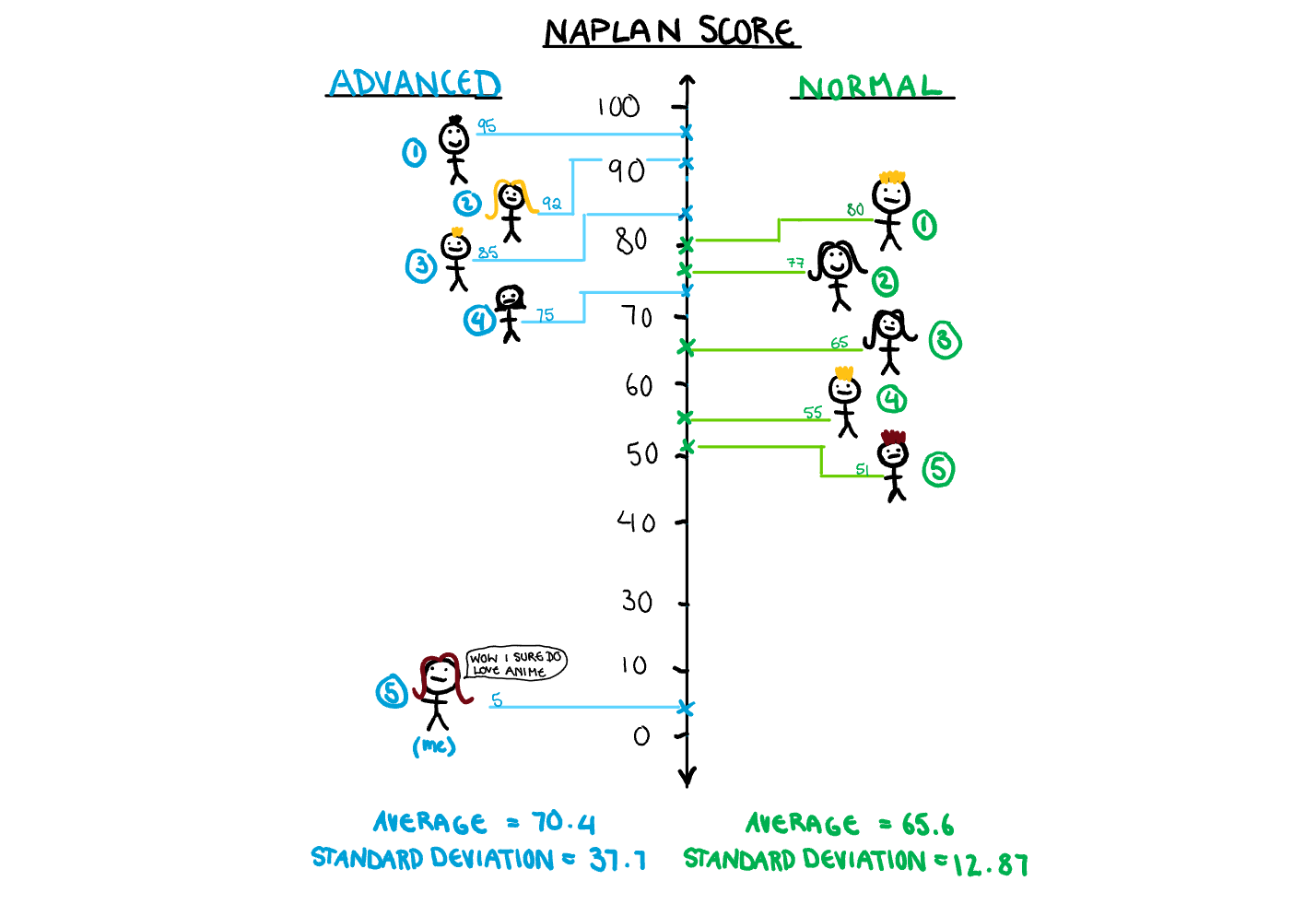
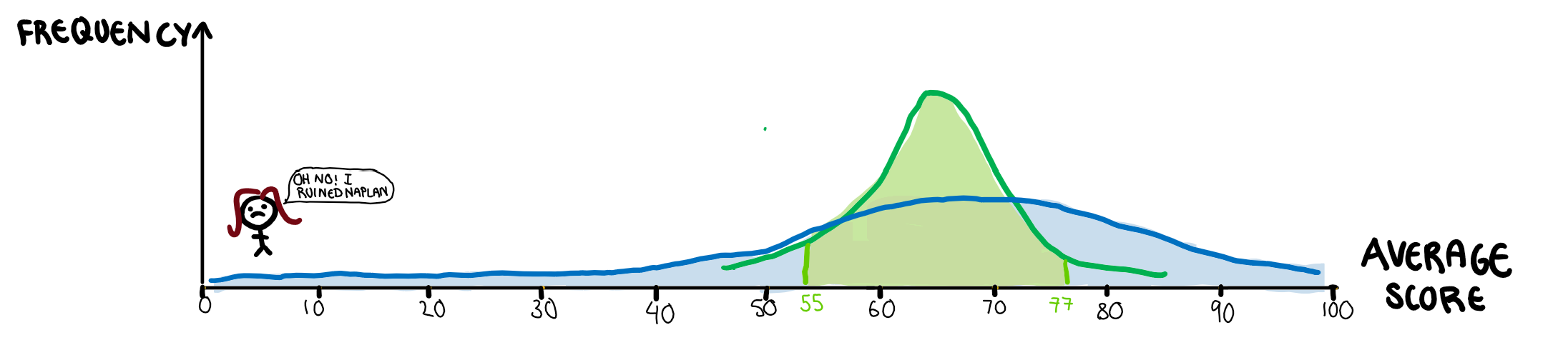
The bootstrap comes to our aid here in two ways. First of all, finding the average of several bootstrapped samples can help with eliminating problems caused out outliers. In this case, since the sample size is only 5, that doesn’t quite work here, but with a sample size that isn’t limited by how many stick figures I can draw, it’s quite useful. Instead, we want to use the median to compare the two classes, since outliers don’t affect it. The problem with the median, is that unlike the mean, it doesn’t have any nice theorems that give us its variance. This is the second way bootstrapping can come to our aid, to create confidence intervals for our median.

To create each bootstrap sample, we will randomly sample our data with replacement 5 times. An example of what one of the bootstrapped samples would look like is shown below.

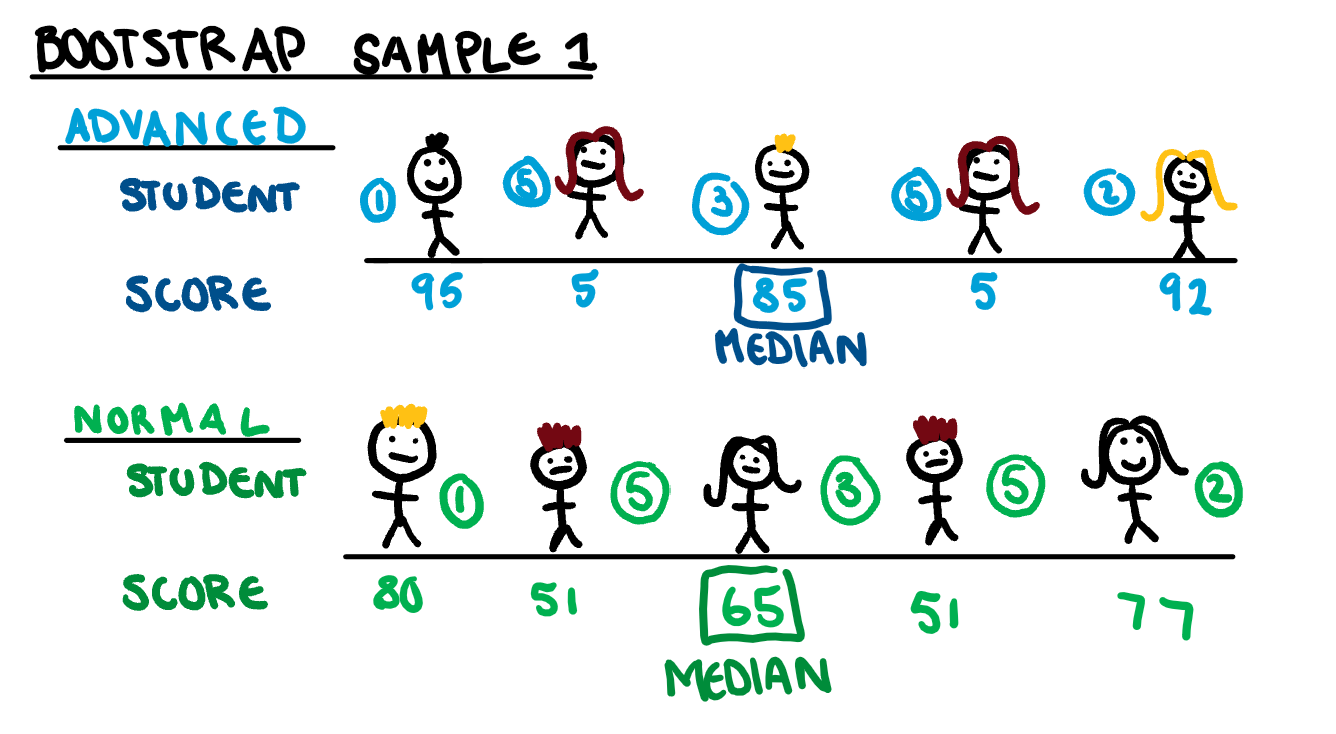
If we repeat this 100 times, we get 100 medians, which we can sort in ascending order, and get a confidence interval for the median. Using this method, we have managed to save my classmates from being dragged down by my terrible paper.

A Final Note

In the end, bootstrapping is a useful and versatile tool, that can help us when we are using less conventional statistics or have an unconventional distribution. Unlike simulation, bootstrapping isn’t generating new data, but rather creating a new simulation from our current data, so the conclusions we can draw aren’t limitless. One place it could be useful, however, is saving the people around me from my moments of stupidity that drag them down to my nearly illiterate level.

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.